According to Einsteins Theory of General Relativity, what is gravity?

Theory of gravity by Albert Einstein

This article is a non-technical introduction to the subject area. For the main encyclopedia commodity, run across General relativity.

High-precision test of full general relativity by the Cassini infinite probe (creative person's impression): radio signals sent betwixt the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Dominicus's mass.

General relativity is a theory of gravitation adult by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational issue between masses results from their warping of spacetime.

By the offset of the 20th century, Newton'due south police of universal gravitation had been accepted for more than 2 hundred years as a valid clarification of the gravitational force betwixt masses. In Newton'south model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that forcefulness, the basic framework was extremely successful at describing motion.

Experiments and observations bear witness that Einstein's description of gravitation accounts for several effects that are unexplained by Newton'southward constabulary, such as infinitesimal anomalies in the orbits of Mercury and other planets. General relativity also predicts novel effects of gravity, such as gravitational waves, gravitational lensing and an effect of gravity on time known as gravitational time dilation. Many of these predictions have been confirmed by experiment or observation, most recently gravitational waves.

Full general relativity has developed into an essential tool in modern astrophysics. It provides the foundation for the current understanding of black holes, regions of space where the gravitational outcome is strong enough that even calorie-free cannot escape. Their strong gravity is thought to be responsible for the intense radiation emitted by certain types of astronomical objects (such as agile galactic nuclei or microquasars). General relativity is also office of the framework of the standard Big Bang model of cosmology.

Although general relativity is non the only relativistic theory of gravity, it is the simplest such theory that is consistent with the experimental information. Nevertheless, a number of open questions remain, the most key of which is how full general relativity tin exist reconciled with the laws of quantum physics to produce a complete and self-consistent theory of quantum gravity.

From special to general relativity [edit]

In September 1905, Albert Einstein published his theory of special relativity, which reconciles Newton's laws of motion with electrodynamics (the interaction betwixt objects with electric accuse). Special relativity introduced a new framework for all of physics past proposing new concepts of space and fourth dimension. Some then-accepted physical theories were inconsistent with that framework; a key example was Newton'due south theory of gravity, which describes the mutual attraction experienced past bodies due to their mass.

Several physicists, including Einstein, searched for a theory that would reconcile Newton's police of gravity and special relativity. Only Einstein'southward theory proved to be consistent with experiments and observations. To understand the theory'due south basic ideas, it is instructive to follow Einstein's thinking between 1907 and 1915, from his simple thought experiment involving an observer in free fall to his fully geometric theory of gravity.^[1]

Equivalence principle [edit]

A person in a free-falling lift experiences weightlessness; objects either float motionless or drift at constant speed. Since everything in the lift is falling together, no gravitational effect tin can be observed. In this way, the experiences of an observer in costless fall are indistinguishable from those of an observer in deep space, far from any significant source of gravity. Such observers are the privileged ("inertial") observers Einstein described in his theory of special relativity: observers for whom calorie-free travels forth direct lines at abiding speed.^[2]

Einstein hypothesized that the similar experiences of weightless observers and inertial observers in special relativity represented a key property of gravity, and he made this the cornerstone of his theory of full general relativity, formalized in his equivalence principle. Roughly speaking, the principle states that a person in a gratis-falling elevator cannot tell that they are in complimentary fall. Every experiment in such a free-falling surround has the same results as it would for an observer at remainder or moving uniformly in deep space, far from all sources of gravity.^[3]

Gravity and acceleration [edit]

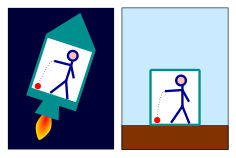
Ball falling to the floor in an accelerating rocket (left) and on Earth (right). The consequence is identical.

Most effects of gravity vanish in complimentary autumn, but furnishings that seem the same as those of gravity can be produced by an accelerated frame of reference. An observer in a closed room cannot tell which of the following is truthful:

• Objects are falling to the flooring because the room is resting on the surface of the Earth and the objects are being pulled down by gravity.
• Objects are falling to the floor because the room is aboard a rocket in space, which is accelerating at nine.81 m/due south², the standard gravity on Earth, and is far from whatsoever source of gravity. The objects are being pulled towards the floor by the aforementioned "inertial force" that presses the driver of an accelerating car into the back of their seat.

Conversely, whatsoever outcome observed in an accelerated reference frame should too be observed in a gravitational field of corresponding forcefulness. This principle allowed Einstein to predict several novel effects of gravity in 1907, as explained in the next department.

An observer in an accelerated reference frame must introduce what physicists call fictitious forces to account for the acceleration experienced by the observer and objects around them. In the case of the driver being pressed into their seat, the force felt by the commuter is one case; another is the force one tin can feel while pulling the arms upwardly and out if attempting to spin around like a top. Einstein's master insight was that the abiding, familiar pull of the World'south gravitational field is fundamentally the same as these fictitious forces.^[four] The apparent magnitude of the fictitious forces ever appears to exist proportional to the mass of any object on which they human action – for instance, the commuter'due south seat exerts but plenty force to accelerate the driver at the same rate as the car. By analogy, Einstein proposed that an object in a gravitational field should feel a gravitational force proportional to its mass, as embodied in Newton's law of gravitation.^[v]

Physical consequences [edit]

In 1907, Einstein was still eight years away from completing the general theory of relativity. All the same, he was able to make a number of novel, testable predictions that were based on his starting point for developing his new theory: the equivalence principle.^[6]

The gravitational redshift of a light wave as it moves upwards against a gravitational field (caused past the yellow star beneath).

The offset new effect is the gravitational frequency shift of lite. Consider 2 observers aboard an accelerating rocket-ship. Aboard such a ship, there is a natural concept of "upward" and "down": the direction in which the transport accelerates is "up", and unattached objects accelerate in the opposite direction, falling "downward". Presume that 1 of the observers is "higher up" than the other. When the lower observer sends a light indicate to the higher observer, the acceleration causes the light to exist reddish-shifted, as may be calculated from special relativity; the second observer will measure a lower frequency for the lite than the get-go. Conversely, calorie-free sent from the college observer to the lower is blueish-shifted, that is, shifted towards higher frequencies.^[7] Einstein argued that such frequency shifts must as well be observed in a gravitational field. This is illustrated in the figure at left, which shows a lite wave that is gradually red-shifted as information technology works its style up against the gravitational acceleration. This result has been confirmed experimentally, as described below.

This gravitational frequency shift corresponds to a gravitational fourth dimension dilation: Since the "higher" observer measures the same calorie-free moving ridge to take a lower frequency than the "lower" observer, time must be passing faster for the higher observer. Thus, time runs more than slowly for observers who are lower in a gravitational field.

Information technology is important to stress that, for each observer, in that location are no appreciable changes of the flow of time for events or processes that are at residuum in his or her reference frame. Five-minute-eggs as timed by each observer's clock take the same consistency; as ane year passes on each clock, each observer ages by that amount; each clock, in short, is in perfect agreement with all processes happening in its immediate vicinity. It is only when the clocks are compared betwixt separate observers that one tin find that time runs more than slowly for the lower observer than for the college.^[8] This result is minute, simply information technology too has been confirmed experimentally in multiple experiments, as described beneath.

In a similar way, Einstein predicted the gravitational deflection of calorie-free: in a gravitational field, light is deflected downward. Quantitatively, his results were off past a cistron of two; the correct derivation requires a more complete formulation of the theory of general relativity, non just the equivalence principle.^[nine]

Tidal effects [edit]

Two bodies falling towards the center of the Earth accelerate towards each other as they fall.

The equivalence between gravitational and inertial effects does not establish a complete theory of gravity. When it comes to explaining gravity about our own location on the Earth's surface, noting that our reference frame is non in free fall, and so that fictitious forces are to be expected, provides a suitable explanation. Only a freely falling reference frame on one side of the Earth cannot explain why the people on the reverse side of the Earth experience a gravitational pull in the contrary direction.

A more basic manifestation of the same effect involves two bodies that are falling side by side towards the Earth. In a reference frame that is in gratis autumn alongside these bodies, they announced to hover weightlessly – but not exactly then. These bodies are non falling in precisely the same direction, only towards a single indicate in infinite: namely, the Earth'southward middle of gravity. Consequently, there is a component of each body's motion towards the other (see the figure). In a small environment such as a freely falling lift, this relative dispatch is minuscule, while for skydivers on opposite sides of the World, the result is big. Such differences in force are also responsible for the tides in the Earth'south oceans, then the term "tidal issue" is used for this phenomenon.

The equivalence between inertia and gravity cannot explain tidal effects – information technology cannot explain variations in the gravitational field.^[10] For that, a theory is needed which describes the way that matter (such as the large mass of the Earth) affects the inertial surroundings around it.

From acceleration to geometry [edit]

In exploring the equivalence of gravity and acceleration equally well as the role of tidal forces, Einstein discovered several analogies with the geometry of surfaces. An example is the transition from an inertial reference frame (in which gratuitous particles coast along straight paths at constant speeds) to a rotating reference frame (in which extra terms respective to fictitious forces have to be introduced in club to explain particle motility): this is analogous to the transition from a Cartesian coordinate system (in which the coordinate lines are straight lines) to a curved coordinate system (where coordinate lines need not be directly).

A deeper illustration relates tidal forces with a property of surfaces called curvature. For gravitational fields, the absence or presence of tidal forces determines whether or non the influence of gravity can be eliminated by choosing a freely falling reference frame. Similarly, the absence or presence of curvature determines whether or non a surface is equivalent to a aeroplane. In the summer of 1912, inspired by these analogies, Einstein searched for a geometric formulation of gravity.^[11]

The elementary objects of geometry – points, lines, triangles – are traditionally defined in three-dimensional space or on two-dimensional surfaces. In 1907, Hermann Minkowski, Einstein's one-time mathematics professor at the Swiss Federal Polytechnic, introduced Minkowski infinite, a geometric conception of Einstein's special theory of relativity where the geometry included non only space but also time. The bones entity of this new geometry is iv-dimensional spacetime. The orbits of moving bodies are curves in spacetime; the orbits of bodies moving at abiding speed without changing direction correspond to directly lines.^[12]

The geometry of full general curved surfaces was developed in the early 19th century by Carl Friedrich Gauss. This geometry had in turn been generalized to higher-dimensional spaces in Riemannian geometry introduced past Bernhard Riemann in the 1850s. With the aid of Riemannian geometry, Einstein formulated a geometric clarification of gravity in which Minkowski's spacetime is replaced by distorted, curved spacetime, only equally curved surfaces are a generalization of ordinary aeroplane surfaces. Embedding Diagrams are used to illustrate curved spacetime in educational contexts.^{[13] [fourteen]}

Subsequently he had realized the validity of this geometric analogy, it took Einstein a further iii years to detect the missing cornerstone of his theory: the equations describing how affair influences spacetime's curvature. Having formulated what are at present known as Einstein's equations (or, more precisely, his field equations of gravity), he presented his new theory of gravity at several sessions of the Prussian University of Sciences in late 1915, culminating in his concluding presentation on November 25, 1915.^[15]

Geometry and gravitation [edit]

Paraphrasing John Wheeler, Einstein'south geometric theory of gravity can exist summarized thus: spacetime tells affair how to move; matter tells spacetime how to curve.^[16] What this means is addressed in the following three sections, which explore the movement of so-called test particles, examine which properties of thing serve as a source for gravity, and, finally, innovate Einstein's equations, which relate these thing backdrop to the curvature of spacetime.

Probing the gravitational field [edit]

Converging geodesics: two lines of longitude (greenish) that start out in parallel at the equator (red) but converge to meet at the pole.

In order to map a torso's gravitational influence, information technology is useful to think almost what physicists telephone call probe or test particles: particles that are influenced by gravity, but are and so small and light that we can neglect their own gravitational effect. In the absence of gravity and other external forces, a test particle moves forth a directly line at a abiding speed. In the language of spacetime, this is equivalent to proverb that such test particles move along direct world lines in spacetime. In the presence of gravity, spacetime is non-Euclidean, or curved, and in curved spacetime straight world lines may not be. Instead, test particles move along lines called geodesics, which are "as direct as possible", that is, they follow the shortest path betwixt starting and catastrophe points, taking the curvature into consideration.

A simple analogy is the post-obit: In geodesy, the science of measuring Earth'due south size and shape, a geodesic (from Greek "geo", Earth, and "daiein", to divide) is the shortest route between two points on the Earth'southward surface. Approximately, such a route is a segment of a great circumvolve, such as a line of longitude or the equator. These paths are certainly not straight, simply because they must follow the curvature of the Earth's surface. Just they are as straight as is possible subject field to this constraint.

The properties of geodesics differ from those of direct lines. For example, on a plane, parallel lines never meet, but this is not then for geodesics on the surface of the Earth: for instance, lines of longitude are parallel at the equator, simply intersect at the poles. Analogously, the world lines of exam particles in gratis fall are spacetime geodesics, the straightest possible lines in spacetime. But however there are crucial differences betwixt them and the truly straight lines that tin exist traced out in the gravity-free spacetime of special relativity. In special relativity, parallel geodesics remain parallel. In a gravitational field with tidal effects, this volition not, in general, be the case. If, for case, two bodies are initially at residual relative to each other, but are so dropped in the Earth'southward gravitational field, they will move towards each other as they autumn towards the Globe'south center.^[17]

Compared with planets and other astronomical bodies, the objects of everyday life (people, cars, houses, even mountains) accept piffling mass. Where such objects are concerned, the laws governing the behavior of test particles are sufficient to describe what happens. Notably, in order to deflect a test particle from its geodesic path, an external strength must be applied. A chair someone is sitting on applies an external upwards strength preventing the person from falling freely towards the center of the World and thus post-obit a geodesic, which they would otherwise be doing without affair in between them and the center of the World. In this way, general relativity explains the daily feel of gravity on the surface of the Earth not every bit the downwards pull of a gravitational forcefulness, just as the upward push of external forces. These forces deflect all bodies resting on the Earth'south surface from the geodesics they would otherwise follow.^[18] For thing objects whose ain gravitational influence cannot be neglected, the laws of move are somewhat more than complicated than for exam particles, although it remains true that spacetime tells matter how to move.^[xix]

Sources of gravity [edit]

In Newton'due south clarification of gravity, the gravitational force is caused by matter. More precisely, information technology is caused by a specific holding of cloth objects: their mass. In Einstein'south theory and related theories of gravitation, curvature at every bespeak in spacetime is too caused past whatever matter is present. Here, too, mass is a key property in determining the gravitational influence of thing. But in a relativistic theory of gravity, mass cannot be the only source of gravity. Relativity links mass with energy, and energy with momentum.

The equivalence between mass and free energy, as expressed by the formula Eastward =mc ^two , is the virtually famous consequence of special relativity. In relativity, mass and energy are two dissimilar ways of describing one physical quantity. If a physical system has energy, it too has the corresponding mass, and vice versa. In detail, all backdrop of a body that are associated with energy, such as its temperature or the binding energy of systems such as nuclei or molecules, contribute to that body's mass, and hence act as sources of gravity.^[xx]

In special relativity, free energy is closely connected to momentum. Simply as space and time are, in that theory, different aspects of a more than comprehensive entity called spacetime, energy and momentum are but different aspects of a unified, four-dimensional quantity that physicists telephone call four-momentum. In consequence, if free energy is a source of gravity, momentum must be a source every bit well. The aforementioned is truthful for quantities that are direct related to energy and momentum, namely internal force per unit area and tension. Taken together, in full general relativity it is mass, energy, momentum, pressure and tension that serve as sources of gravity: they are how matter tells spacetime how to curve. In the theory's mathematical formulation, all these quantities are merely aspects of a more general physical quantity chosen the energy–momentum tensor.^[21]

Einstein'due south equations [edit]

Einstein'southward equations are the centerpiece of general relativity. They provide a precise formulation of the human relationship between spacetime geometry and the backdrop of matter, using the linguistic communication of mathematics. More concretely, they are formulated using the concepts of Riemannian geometry, in which the geometric properties of a space (or a spacetime) are described by a quantity called a metric. The metric encodes the information needed to compute the central geometric notions of distance and angle in a curved space (or spacetime).

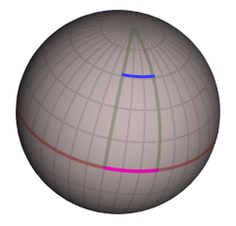
Distances, at different latitudes, corresponding to 30 degrees difference in longitude.

A spherical surface like that of the World provides a uncomplicated instance. The location of any point on the surface can exist described by ii coordinates: the geographic latitude and longitude. Different the Cartesian coordinates of the plane, coordinate differences are non the same as distances on the surface, every bit shown in the diagram on the right: for someone at the equator, moving xxx degrees of longitude westward (magenta line) corresponds to a distance of roughly 3,300 kilometers (2,100 mi), while for someone at a latitude of 55 degrees, moving thirty degrees of longitude westward (blue line) covers a distance of merely ane,900 kilometers (one,200 mi). Coordinates therefore do not provide plenty information to depict the geometry of a spherical surface, or indeed the geometry of any more complicated space or spacetime. That data is precisely what is encoded in the metric, which is a part divers at each point of the surface (or space, or spacetime) and relates coordinate differences to differences in distance. All other quantities that are of involvement in geometry, such as the length of any given curve, or the angle at which two curves meet, tin be computed from this metric function.^[22]

The metric function and its rate of alter from point to point can be used to ascertain a geometrical quantity called the Riemann curvature tensor, which describes exactly how the Riemannian manifold, the spacetime in the theory of relativity, is curved at each bespeak. Every bit has already been mentioned, the matter content of the spacetime defines some other quantity, the energy–momentum tensor T, and the principle that "spacetime tells matter how to move, and affair tells spacetime how to bend" means that these quantities must be related to each other. Einstein formulated this relation past using the Riemann curvature tensor and the metric to define some other geometrical quantity G, now chosen the Einstein tensor, which describes some aspects of the way spacetime is curved. Einstein's equation then states that

${\displaystyle \mathbf {Thou} ={\frac {8\pi Chiliad}{c^{4}}}\mathbf {T} ,}$

i.east., up to a constant multiple, the quantity Grand (which measures curvature) is equated with the quantity T (which measures affair content). Here, 1000 is the gravitational abiding of Newtonian gravity, and c is the speed of light from special relativity.

This equation is often referred to in the plural equally Einstein's equations, since the quantities 1000 and T are each determined past several functions of the coordinates of spacetime, and the equations equate each of these component functions.^[23] A solution of these equations describes a particular geometry of spacetime; for example, the Schwarzschild solution describes the geometry around a spherical, not-rotating mass such as a star or a black hole, whereas the Kerr solution describes a rotating black hole. Still other solutions can describe a gravitational wave or, in the instance of the Friedmann–Lemaître–Robertson–Walker solution, an expanding universe. The simplest solution is the uncurved Minkowski spacetime, the spacetime described past special relativity.^[24]

Experiments [edit]

No scientific theory is cocky-evidently true; each is a model that must be checked by experiment. Newton's law of gravity was accepted because it accounted for the motion of planets and moons in the Solar Organisation with considerable accuracy. As the precision of experimental measurements gradually improved, some discrepancies with Newton'south predictions were observed, and these were accounted for in the general theory of relativity. Similarly, the predictions of full general relativity must as well exist checked with experiment, and Einstein himself devised iii tests now known as the classical tests of the theory:

Newtonian (cherry) vs. Einsteinian orbit (blue) of a single planet orbiting a spherical star.

• Newtonian gravity predicts that the orbit which a single planet traces around a perfectly spherical star should be an ellipse. Einstein's theory predicts a more complicated curve: the planet behaves as if it were travelling around an ellipse, but at the aforementioned time, the ellipse as a whole is rotating slowly around the star. In the diagram on the correct, the ellipse predicted by Newtonian gravity is shown in red, and part of the orbit predicted by Einstein in blueish. For a planet orbiting the Sun, this deviation from Newton's orbits is known every bit the anomalous perihelion shift. The first measurement of this event, for the planet Mercury, dates back to 1859. The almost authentic results for Mercury and for other planets to appointment are based on measurements which were undertaken between 1966 and 1990, using radio telescopes.^[25] General relativity predicts the right dissonant perihelion shift for all planets where this tin be measured accurately (Mercury, Venus and the Earth).
• Co-ordinate to full general relativity, low-cal does non travel along direct lines when it propagates in a gravitational field. Instead, it is deflected in the presence of massive bodies. In particular, starlight is deflected as it passes near the Sun, leading to credible shifts of upward ane.75 arc seconds in the stars' positions in the sky (an arc 2d is equal to one/3600 of a degree). In the framework of Newtonian gravity, a heuristic argument can exist fabricated that leads to low-cal deflection by half that amount. The different predictions can be tested by observing stars that are close to the Sunday during a solar eclipse. In this style, a British expedition to West Africa in 1919, directed by Arthur Eddington, confirmed that Einstein's prediction was right, and the Newtonian predictions wrong, via observation of the May 1919 eclipse. Eddington's results were not very authentic; subsequent observations of the deflection of the light of distant quasars by the Dominicus, which utilize highly authentic techniques of radio astronomy, have confirmed Eddington's results with significantly amend precision (the outset such measurements date from 1967, the most recent comprehensive analysis from 2004).^[26]
• Gravitational redshift was commencement measured in a laboratory setting in 1959 by Pound and Rebka. It is too seen in astrophysical measurements, notably for lite escaping the white dwarf Sirius B. The related gravitational time dilation effect has been measured by transporting atomic clocks to altitudes of between tens and tens of thousands of kilometers (first by Hafele and Keating in 1971; most accurately to date by Gravity Probe A launched in 1976).^[27]

Of these tests, merely the perihelion advance of Mercury was known prior to Einstein's final publication of full general relativity in 1916. The subsequent experimental confirmation of his other predictions, specially the first measurements of the deflection of light by the sun in 1919, catapulted Einstein to international stardom.^[28] These iii experiments justified adopting general relativity over Newton's theory and, incidentally, over a number of alternatives to general relativity that had been proposed.

Further tests of general relativity include precision measurements of the Shapiro consequence or gravitational fourth dimension delay for light, measured in 2002 past the Cassini space probe. Ane set of tests focuses on effects predicted past full general relativity for the behavior of gyroscopes travelling through space. One of these effects, geodetic precession, has been tested with the Lunar Laser Ranging Experiment (loftier-precision measurements of the orbit of the Moon). Some other, which is related to rotating masses, is called frame-dragging. The geodetic and frame-dragging furnishings were both tested by the Gravity Probe B satellite experiment launched in 2004, with results confirming relativity to within 0.5% and 15%, respectively, every bit of Dec 2008.^[29]

Past cosmic standards, gravity throughout the solar system is weak. Since the differences between the predictions of Einstein'due south and Newton's theories are most pronounced when gravity is strong, physicists have long been interested in testing various relativistic effects in a setting with comparatively stiff gravitational fields. This has become possible thanks to precision observations of binary pulsars. In such a star arrangement, 2 highly compact neutron stars orbit each other. At least one of them is a pulsar – an astronomical object that emits a tight beam of radiowaves. These beams strike the Earth at very regular intervals, similarly to the style that the rotating beam of a lighthouse ways that an observer sees the lighthouse blink, and tin exist observed as a highly regular series of pulses. Full general relativity predicts specific deviations from the regularity of these radio pulses. For instance, at times when the radio waves pass shut to the other neutron star, they should exist deflected by the star's gravitational field. The observed pulse patterns are impressively close to those predicted by full general relativity.^[30]

Ane item set up of observations is related to eminently useful practical applications, namely to satellite navigation systems such as the Global Positioning Organization that are used for both precise positioning and timekeeping. Such systems rely on ii sets of diminutive clocks: clocks aboard satellites orbiting the Earth, and reference clocks stationed on the Earth's surface. General relativity predicts that these ii sets of clocks should tick at slightly different rates, due to their unlike motions (an effect already predicted by special relativity) and their different positions inside the Earth'due south gravitational field. In gild to ensure the organisation's accuracy, either the satellite clocks are slowed down past a relativistic gene, or that same factor is fabricated part of the evaluation algorithm. In turn, tests of the arrangement'south accuracy (especially the very thorough measurements that are office of the definition of universal coordinated time) are testament to the validity of the relativistic predictions.^[31]

A number of other tests have probed the validity of various versions of the equivalence principle; strictly speaking, all measurements of gravitational time dilation are tests of the weak version of that principle, not of general relativity itself. So far, full general relativity has passed all observational tests.^[32]

Astrophysical applications [edit]

Models based on general relativity play an important role in astrophysics; the success of these models is further attestation to the theory'south validity.

Gravitational lensing [edit]

Since light is deflected in a gravitational field, it is possible for the low-cal of a afar object to achieve an observer along ii or more paths. For instance, calorie-free of a very distant object such every bit a quasar can laissez passer along one side of a massive galaxy and exist deflected slightly so as to reach an observer on Globe, while low-cal passing along the opposite side of that same galaxy is deflected likewise, reaching the same observer from a slightly unlike direction. Every bit a effect, that detail observer will see one astronomical object in two different places in the night sky. This kind of focussing is well known when it comes to optical lenses, and hence the respective gravitational effect is called gravitational lensing.^[33]

Observational astronomy uses lensing furnishings as an of import tool to infer properties of the lensing object. Fifty-fifty in cases where that object is not directly visible, the shape of a lensed paradigm provides data about the mass distribution responsible for the lite deflection. In detail, gravitational lensing provides one manner to measure the distribution of dark matter, which does not give off light and can be observed but by its gravitational furnishings. One particularly interesting application are big-calibration observations, where the lensing masses are spread out over a significant fraction of the observable universe, and tin can be used to obtain information near the large-calibration properties and development of our cosmos.^[34]

Gravitational waves [edit]

Gravitational waves, a directly consequence of Einstein's theory, are distortions of geometry that propagate at the speed of low-cal, and can be idea of as ripples in spacetime. They should not be confused with the gravity waves of fluid dynamics, which are a different concept.

In February 2016, the Avant-garde LIGO team announced that they had directly observed gravitational waves from a blackness pigsty merger.^[35]

Indirectly, the result of gravitational waves had been detected in observations of specific binary stars. Such pairs of stars orbit each other and, as they do and then, gradually lose free energy by emitting gravitational waves. For ordinary stars like the Sun, this free energy loss would be likewise modest to be detectable, but this free energy loss was observed in 1974 in a binary pulsar called PSR1913+16. In such a organisation, one of the orbiting stars is a pulsar. This has two consequences: a pulsar is an extremely dense object known as a neutron star, for which gravitational moving ridge emission is much stronger than for ordinary stars. Also, a pulsar emits a narrow axle of electromagnetic radiations from its magnetic poles. Equally the pulsar rotates, its beam sweeps over the Earth, where it is seen every bit a regular series of radio pulses, simply as a transport at body of water observes regular flashes of light from the rotating light in a lighthouse. This regular pattern of radio pulses functions as a highly accurate "clock". It can be used to time the double star'southward orbital flow, and it reacts sensitively to distortions of spacetime in its firsthand neighborhood.

The discoverers of PSR1913+16, Russell Hulse and Joseph Taylor, were awarded the Nobel Prize in Physics in 1993. Since then, several other binary pulsars have been found. The most useful are those in which both stars are pulsars, since they provide accurate tests of full general relativity.^[36]

Currently, a number of land-based gravitational wave detectors are in functioning, and a mission to launch a infinite-based detector, LISA, is currently under development, with a precursor mission (LISA Pathfinder) which was launched in 2015. Gravitational wave observations can be used to obtain information about compact objects such as neutron stars and black holes, and also to probe the land of the early universe fractions of a second after the Big Bang.^[37]

Black holes [edit]

Blackness hole-powered jet emanating from the central region of the galaxy M87.

When mass is concentrated into a sufficiently compact region of space, general relativity predicts the germination of a black hole – a region of space with a gravitational effect and then strong that not even lite tin escape. Sure types of black holes are thought to be the final state in the development of massive stars. On the other mitt, supermassive black holes with the mass of millions or billions of Suns are assumed to reside in the cores of most galaxies, and they play a primal role in electric current models of how galaxies have formed over the past billions of years.^[38]

Thing falling onto a compact object is one of the nearly efficient mechanisms for releasing free energy in the form of radiation, and thing falling onto black holes is thought to be responsible for some of the brightest astronomical phenomena imaginable. Notable examples of bang-up interest to astronomers are quasars and other types of active galactic nuclei. Under the right conditions, falling matter accumulating around a black pigsty can lead to the germination of jets, in which focused beams of matter are flung away into infinite at speeds nearly that of light.^[39]

There are several properties that make black holes the most promising sources of gravitational waves. 1 reason is that black holes are the near meaty objects that can orbit each other every bit role of a binary system; equally a result, the gravitational waves emitted by such a system are specially strong. Another reason follows from what are chosen black-hole uniqueness theorems: over time, black holes retain merely a minimal ready of distinguishing features (these theorems accept become known as "no-hair" theorems), regardless of the starting geometric shape. For example, in the long term, the collapse of a hypothetical affair cube will not result in a cube-shaped black hole. Instead, the resulting blackness hole will be duplicate from a black pigsty formed by the collapse of a spherical mass. In its transition to a spherical shape, the black hole formed past the collapse of a more complicated shape volition emit gravitational waves.^[40]

Cosmology [edit]

An paradigm, created using information from the WMAP satellite telescope, of the radiation emitted no more a few hundred thousand years after the Big Bang.

Ane of the most of import aspects of general relativity is that it can exist applied to the universe as a whole. A key point is that, on big scales, our universe appears to be constructed along very elementary lines: all current observations suggest that, on average, the construction of the creation should be approximately the same, regardless of an observer's location or direction of observation: the universe is approximately homogeneous and isotropic. Such insufficiently unproblematic universes can be described past simple solutions of Einstein'due south equations. The current cosmological models of the universe are obtained by combining these uncomplicated solutions to general relativity with theories describing the properties of the universe's thing content, namely thermodynamics, nuclear- and particle physics. According to these models, our nowadays universe emerged from an extremely dense high-temperature state – the Large Bang – roughly 14 billion years ago and has been expanding ever since.^[41]

Einstein'south equations can be generalized by calculation a term called the cosmological constant. When this term is present, empty space itself acts every bit a source of attractive (or, less normally, repulsive) gravity. Einstein originally introduced this term in his pioneering 1917 paper on cosmology, with a very specific motivation: contemporary cosmological idea held the universe to be static, and the additional term was required for constructing static model universes within the framework of general relativity. When it became credible that the universe is not static, but expanding, Einstein was quick to discard this additional term. Since the stop of the 1990s, however, astronomical evidence indicating an accelerating expansion consistent with a cosmological constant – or, equivalently, with a particular and ubiquitous kind of dark energy – has steadily been accumulating.^[42]

Modern research [edit]

General relativity is very successful in providing a framework for accurate models which describe an impressive array of physical phenomena. On the other manus, there are many interesting open questions, and in particular, the theory as a whole is virtually certainly incomplete.^[43]

In contrast to all other mod theories of cardinal interactions, general relativity is a classical theory: it does non include the effects of quantum physics. The quest for a quantum version of general relativity addresses ane of the well-nigh cardinal open questions in physics. While at that place are promising candidates for such a theory of breakthrough gravity, notably string theory and loop quantum gravity, there is at present no consequent and complete theory. It has long been hoped that a theory of breakthrough gravity would as well eliminate another problematic feature of full general relativity: the presence of spacetime singularities. These singularities are boundaries ("sharp edges") of spacetime at which geometry becomes ill-defined, with the consequence that general relativity itself loses its predictive ability. Furthermore, at that place are and so-called singularity theorems which predict that such singularities must exist within the universe if the laws of general relativity were to concord without whatsoever quantum modifications. The all-time-known examples are the singularities associated with the model universes that describe black holes and the starting time of the universe.^[44]

Other attempts to alter full general relativity have been made in the context of cosmology. In the modern cosmological models, most energy in the universe is in forms that have never been detected direct, namely dark energy and dark matter. At that place have been several controversial proposals to remove the need for these enigmatic forms of matter and energy, by modifying the laws governing gravity and the dynamics of cosmic expansion, for example modified Newtonian dynamics.^[45]

Beyond the challenges of quantum effects and cosmology, enquiry on general relativity is rich with possibilities for farther exploration: mathematical relativists explore the nature of singularities and the fundamental properties of Einstein's equations,^[46] and e'er more comprehensive computer simulations of specific spacetimes (such every bit those describing merging black holes) are run.^[47] More than 1 hundred years after the theory was first published, enquiry is more active than e'er.^[48]

Encounter also [edit]

• Full general relativity
• Introduction to the mathematics of general relativity
• Introduction to special relativity
• History of general relativity
• Tests of full general relativity
• Numerical relativity
• Derivations of the Lorentz transformations
• Listing of books on general relativity

References [edit]

1. ^ This development is traced e.g. in Renn 2005, p. 110ff., in chapters nine through 15 of Pais 1982, and in Janssen 2005. A precis of Newtonian gravity can be plant in Schutz 2003, chapters 2–four. It is impossible to say whether the problem of Newtonian gravity crossed Einstein'southward listen earlier 1907, merely, by his ain access, his outset serious attempts to reconcile that theory with special relativity date to that yr, cf. Pais 1982, p. 178.
2. ^ This is described in particular in chapter 2 of Wheeler 1990.
3. ^ While the equivalence principle is yet role of modern expositions of general relativity, there are some differences between the modern version and Einstein'south original concept, cf. Norton 1985.
4. ^ E. g. Janssen 2005, p. 64f. Einstein himself as well explains this in section Xx of his not-technical book Einstein 1961. Following earlier ideas by Ernst Mach, Einstein besides explored centrifugal forces and their gravitational analogue, cf. Stachel 1989.
5. ^ Einstein explained this in section Xx of Einstein 1961. He considered an object "suspended" by a rope from the ceiling of a room aboard an accelerating rocket: from within the room it looks as if gravitation is pulling the object down with a forcefulness proportional to its mass, merely from outside the rocket information technology looks every bit if the rope is simply transferring the acceleration of the rocket to the object, and must therefore exert just the "forcefulness" to do then.
6. ^ More specifically, Einstein's calculations, which are described in chapter 11b of Pais 1982, utilise the equivalence principle, the equivalence of gravity and inertial forces, and the results of special relativity for the propagation of light and for accelerated observers (the latter past considering, at each moment, the instantaneous inertial frame of reference associated with such an accelerated observer).
7. ^ This effect tin can be derived direct within special relativity, either past looking at the equivalent situation of two observers in an accelerated rocket-ship or by looking at a falling elevator; in both situations, the frequency shift has an equivalent description as a Doppler shift between sure inertial frames. For simple derivations of this, see Harrison 2002.
8. ^ See chapter 12 of Mermin 2005.
9. ^ Cf. Ehlers & Rindler 1997; for a non-technical presentation, meet Pössel 2007.
10. ^ These and other tidal effects are described in Wheeler 1990, pp. 83–91.
11. ^ Tides and their geometric interpretation are explained in chapter 5 of Wheeler 1990. This office of the historical development is traced in Pais 1982, department 12b.
12. ^ For elementary presentations of the concept of spacetime, see the first department in chapter two of Thorne 1994, and Greene 2004, p. 47–61. More complete treatments on a fairly unproblematic level can exist found e.g. in Mermin 2005 and in Wheeler 1990, chapters 8 and 9.
13. ^ Marolf, Donald (1999). "Spacetime Embedding Diagrams for Black Holes". General Relativity and Gravitation. 31 (half dozen): 919–944. arXiv:gr-qc/9806123. Bibcode:1999GReGr..31..919M. doi:10.1023/A:1026646507201. S2CID 12502462.
14. ^ See Wheeler 1990, chapters 8 and nine for vivid illustrations of curved spacetime.
15. ^ Einstein's struggle to find the correct field equations is traced in chapters 13–xv of Pais 1982.
16. ^ East.g. p. 11 in Wheeler 1990.
17. ^ A thorough, nevertheless attainable business relationship of basic differential geometry and its application in full general relativity can be establish in Geroch 1978.
18. ^ Run into affiliate 10 of Wheeler 1990.
19. ^ In fact, when starting from the complete theory, Einstein's equation tin exist used to derive these more complicated laws of motility for thing as a consequence of geometry, but deriving from this the motility of idealized exam particles is a highly non-trivial task, cf. Poisson 2004.
20. ^ A simple caption of mass–energy equivalence can be found in sections 3.8 and 3.9 of Giulini 2005.
21. ^ See chapter 6 of Wheeler 1990.
22. ^ For a more than detailed definition of the metric, merely one that is more informal than a textbook presentation, meet chapter xiv.iv of Penrose 2004.
23. ^ The geometrical meaning of Einstein's equations is explored in capacity 7 and 8 of Wheeler 1990; cf. box 2.6 in Thorne 1994. An introduction using merely very simple mathematics is given in chapter 19 of Schutz 2003.
24. ^ The nigh important solutions are listed in every textbook on full general relativity; for a (technical) summary of our current understanding, see Friedrich 2005.
25. ^ More precisely, these are VLBI measurements of planetary positions; meet affiliate v of Will 1993 and section 3.five of Volition 2006.
26. ^ For the historical measurements, encounter Hartl 2005, Kennefick 2005, and Kennefick 2007; Soldner'south original derivation in the framework of Newton'due south theory is von Soldner 1804. For the most precise measurements to date, encounter Bertotti 2005.
27. ^ See Kennefick 2005 and chapter iii of Volition 1993. For the Sirius B measurements, meet Trimble & Barstow 2007.
28. ^ Pais 1982, Mercury on pp. 253–254, Einstein's ascent to fame in sections 16b and 16c.
29. ^ Everitt, C.W.F.; Parkinson, B.W. (2009), Gravity Probe B Science Results—NASA Final Report (PDF) , retrieved 2009-05-02
30. ^ Kramer 2004.
31. ^ An attainable business relationship of relativistic furnishings in the global positioning arrangement can be found in Ashby 2002; details are given in Ashby 2003.
32. ^ An accessible introduction to tests of general relativity is Will 1993; a more technical, up-to-date account is Will 2006.
33. ^ The geometry of such situations is explored in chapter 23 of Schutz 2003.
34. ^ Introductions to gravitational lensing and its applications can be plant on the webpages Newbury 1997 and Lochner 2007.
35. ^ B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger". Physical Review Letters. 116 (half-dozen): 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. doi:ten.1103/PhysRevLett.116.061102. PMID 26918975. S2CID 124959784. {{cite periodical}}: CS1 maint: uses authors parameter (link)
36. ^ Schutz 2003, pp. 317–321; Bartusiak 2000, pp. 70–86.
37. ^ The ongoing search for gravitational waves is described in Bartusiak 2000 and in Blair & McNamara 1997.
38. ^ For an overview of the history of black hole physics from its beginnings in the early 20th century to modern times, see the very readable account by Thorne 1994. For an up-to-date account of the role of black holes in structure germination, see Springel et al. 2005; a brief summary can exist constitute in the related article Gnedin 2005.
39. ^ See chapter 8 of Sparke & Gallagher 2007 and Disney 1998. A treatment that is more thorough, yet involves but comparatively little mathematics can exist establish in Robson 1996.
40. ^ An uncomplicated introduction to the black hole uniqueness theorems can be constitute in Chrusciel 2006 and in Thorne 1994, pp. 272–286.
41. ^ Detailed information tin be found in Ned Wright'southward Cosmology Tutorial and FAQ, Wright 2007; a very readable introduction is Hogan 1999. Using undergraduate mathematics but avoiding the avant-garde mathematical tools of general relativity, Berry 1989 provides a more thorough presentation.
42. ^ Einstein's original newspaper is Einstein 1917; good descriptions of more modern developments tin can be establish in Cowen 2001 and Caldwell 2004.
43. ^ Cf. Maddox 1998, pp. 52–59 and 98–122; Penrose 2004, section 34.1 and chapter 30.
44. ^ With a focus on string theory, the search for quantum gravity is described in Greene 1999; for an account from the bespeak of view of loop breakthrough gravity, see Smolin 2001.
45. ^ For nighttime matter, see Milgrom 2002; for dark energy, Caldwell 2004
46. ^ Come across Friedrich 2005.
47. ^ A review of the various problems and the techniques being adult to overcome them, see Lehner 2002.
48. ^ A practiced starting bespeak for a snapshot of present-day research in relativity is the electronic review journal Living Reviews in Relativity.

Bibliography [edit]

• Ashby, Neil (2002), "Relativity and the Global Positioning System" (PDF), Physics Today, 55 (5): 41–47, Bibcode:2002PhT....55e..41A, doi:10.1063/1.1485583, PMC5253894, PMID 28163638
• Ashby, Neil (2003), "Relativity in the Global Positioning Organization", Living Reviews in Relativity, 6 (1): 1, Bibcode:2003LRR.....half dozen....1A, doi:10.12942/lrr-2003-1, PMC5253894, PMID 28163638, archived from the original on 2007-07-04, retrieved 2007-07-06
• Bartusiak, Marcia (2000), Einstein'southward Unfinished Symphony: Listening to the Sounds of Space-Time, Berkley, ISBN978-0-425-18620-6
• Drupe, Michael V. (1989), Principles of Cosmology and Gravitation (1989 reprinted ed.), Institute of Physics Publishing, ISBN0-85274-037-nine
• Bertotti, Bruno (2005), "The Cassini Experiment: Investigating the Nature of Gravity", in Renn, Jürgen (ed.), One hundred authors for Einstein, Wiley-VCH, pp. 402–405, ISBN3-527-40574-seven
• Blair, David; McNamara, Geoff (1997), Ripples on a Cosmic Ocean. The Search for Gravitational Waves, Perseus, ISBN0-7382-0137-five
• Caldwell, Robert R. (2004), "Dark Energy", Physics Globe, 17 (v): 37–42, doi:10.1088/2058-7058/17/five/36
• Chrusciel, Piotr (2006), "How many different kinds of blackness hole are in that location?", Einstein Online, archived from the original on 2011-04-14, retrieved 2007-07-15
• Cowen, Ron (2001), "A Night Force in the Universe", Science News, Society for Science &#38, 159 (14): 218–220, doi:10.2307/3981642, JSTOR 3981642
• Disney, Michael (1998), "A New Wait at Quasars", Scientific American, 278 (6): 52–57, Bibcode:1998SciAm.278f..52D, doi:10.1038/scientificamerican0698-52
• Ehlers, Jürgen; Rindler, Wolfgang (1997), "Local and Global Light Bending in Einstein's and other Gravitational Theories", General Relativity and Gravitation, 29 (4): 519–529, Bibcode:1997GReGr..29..519E, doi:10.1023/A:1018843001842, hdl:11858/00-001M-0000-0013-5AB5-4, S2CID 118162303
• Einstein, Albert (1917), "Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie", Sitzungsberichte der Preußischen Akademie der Wissenschaften: 142
• Einstein, Albert (1961), Relativity. The special and general theory, Crown Publishers
• Friedrich, Helmut (2005), "Is general relativity 'substantially understood'?", Annalen der Physik, 15 (1–ii): 84–108, arXiv:gr-qc/0508016, Bibcode:2006AnP...518...84F, doi:ten.1002/andp.200510173, S2CID 37236624
• Geroch, Robert (1978), General relativity from A to B, Academy of Chicago Press, ISBN0-226-28864-i
• Giulini, Domenico (2005), Special relativity. A first see, Oxford University Press, ISBN0-19-856746-four
• Gnedin, Nickolay Y. (2005), "Digitizing the Universe", Nature, 435 (7042): 572–573, Bibcode:2005Natur.435..572G, doi:10.1038/435572a, PMID 15931201, S2CID 3023436
• Greene, Brian (1999), The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory , Vintage, ISBN0-375-70811-1
• Greene, Brian (2004), The Fabric of the Cosmos: Space, Time, and the Texture of Reality, A. A. Knopf, Bibcode:2004fcst.book.....Yard, ISBN0-375-41288-iii
• Harrison, David Thousand. (2002), A Not-mathematical Proof of Gravitational Fourth dimension Dilation (PDF) , retrieved 2007-05-06
• Hartl, Gerhard (2005), "The Confirmation of the General Theory of Relativity by the British Eclipse Expedition of 1919", in Renn, Jürgen (ed.), One hundred authors for Einstein, Wiley-VCH, pp. 182–187, ISBN3-527-40574-7
• Hogan, Craig J. (1999), The Piffling Book of the Big Bang. A Cosmic Primer , Springer, ISBN0-387-98385-half dozen
• Janssen, Michel (2005), "Of pots and holes: Einstein's bumpy road to general relativity" (PDF), Annalen der Physik, fourteen (S1): 58–85, Bibcode:2005AnP...517S..58J, doi:10.1002/andp.200410130
• Kennefick, Daniel (2005), "Astronomers Test General Relativity: Lite-bending and the Solar Redshift", in Renn, Jürgen (ed.), Ane hundred authors for Einstein, Wiley-VCH, pp. 178–181, ISBNiii-527-40574-7
• Kennefick, Daniel (2007), "Non Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition", Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005, vol. 0709, p. 685, arXiv:0709.0685, Bibcode:2007arXiv0709.0685K, doi:10.1016/j.shpsa.2012.07.010, S2CID 119203172
• Kramer, Michael (2004), "Millisecond Pulsars as Tools of Central Physics", in Karshenboim, South. K.; Peik, Eastward. (eds.), Astrophysics, Clocks and Key Constants (Lecture Notes in Physics Vol. 648), Springer, pp. 33–54 (E-Impress at astro-ph/0405178)
• Lehner, Luis (2002), "Numerical Relativity: Status and Prospects", Proceedings of the 16th International Briefing on General Relativity and Gravitation, held fifteen–21 July 2001 in Durban, p. 210, arXiv:gr-qc/0202055, Bibcode:2002grg..conf..210L, doi:10.1142/9789812776556_0010, ISBN978-981-238-171-two, S2CID 9145148
• Lochner, Jim, ed. (2007), "Gravitational Lensing", Imagine the Universe Website, NASA GSFC, archived from the original on 2007-06-17, retrieved 2007-06-12
• Maddox, John (1998), What Remains To Be Discovered, Macmillan, ISBN0-684-82292-X
• Mermin, Northward. David (2005), Information technology's Near Time. Understanding Einstein'southward Relativity , Princeton University Printing, ISBN0-691-12201-6
• Milgrom, Mordehai (2002), "Does nighttime affair really exist?", Scientific American, 287 (2): xxx–37, Bibcode:2002SciAm.287b..42M, doi:ten.1038/scientificamerican0802-42, PMID 12140952, archived from the original on 2011-06-10, retrieved 2007-06-13
• Norton, John D. (1985), "What was Einstein's principle of equivalence?" (PDF), Studies in History and Philosophy of Science, 16 (3): 203–246, Bibcode:1985SHPSA..sixteen..203N, doi:10.1016/0039-3681(85)90002-0, retrieved 2007-06-11
• Newbury, Pete (1997), Gravitational lensing webpages, archived from the original on 2012-12-06, retrieved 2007-06-12
• Nieto, Michael Martin (2006), "The quest to understand the Pioneer bibelot" (PDF), EurophysicsNews, 37 (6): thirty–34, arXiv:gr-qc/0702017, Bibcode:2006ENews..37...30N, doi:10.1051/epn:2006604, S2CID 118949889, archived from the original (PDF) on 2007-06-29
• Pais, Abraham (1982), 'Subtle is the Lord ...' The Science and life of Albert Einstein, Oxford University Press, ISBN0-nineteen-853907-10
• Penrose, Roger (2004), The Route to Reality, A. A. Knopf, ISBN0-679-45443-eight
• Pössel, Grand. (2007), "The equivalence principle and the deflection of light", Einstein Online, archived from the original on 2007-05-03, retrieved 2007-05-06
• Poisson, Eric (2004), "The Movement of Indicate Particles in Curved Spacetime", Living Rev. Relativ., 7 (1): half dozen, arXiv:gr-qc/0306052, Bibcode:2004LRR.....7....6P, doi:10.12942/lrr-2004-six, PMC5256043, PMID 28179866
• Renn, Jürgen, ed. (2005), Albert Einstein – Primary Engineer of the Universe: Einstein's Life and Piece of work in Context, Berlin: Wiley-VCH, ISBN3-527-40571-2
• Robson, Ian (1996), Active galactic nuclei, John Wiley, ISBN0-471-95853-0
• Schutz, Bernard F. (2003), Gravity from the basis upwardly, Cambridge Academy Printing, ISBN0-521-45506-5
• Smolin, Lee (2001), 3 Roads to Breakthrough Gravity, Bones, ISBN0-465-07835-4
• von Soldner, Johann Georg (1804), "Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht", Berliner Astronomisches Jahrbuch: 161–172 .
• Sparke, Linda S.; Gallagher, John S. (2007), Galaxies in the universe – An introduction, Cambridge University Press, Bibcode:2007gitu.book.....Due south, ISBN978-0-521-85593-8
• Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos South.; Yoshida, N; Gao, L; Navarro, J; Thacker, R; Croton, D; et al. (2005), "Simulations of the formation, evolution and clustering of galaxies and quasars" (PDF), Nature, 435 (7042): 629–636, arXiv:astro-ph/0504097, Bibcode:2005Natur.435..629S, doi:10.1038/nature03597, hdl:2027.42/62586, PMID 15931216, S2CID 4383030
• Stachel, John (1989), "The Rigidly Rotating Disk equally the 'Missing Link in the History of General Relativity'", in Howard, D.; Stachel, J. (eds.), Einstein and the History of Full general Relativity (Einstein Studies, Vol. 1), Birkhäuser, pp. 48–62, ISBN0-8176-3392-eight
• Thorne, Kip (1994), Black Holes and Time Warps: Einstein's Outrageous Legacy, W W Norton & Company, ISBN0-393-31276-three
• Trimble, Virginia; Barstow, Martin (2007), "Gravitational redshift and White Dwarf stars", Einstein Online, archived from the original on 2011-08-28, retrieved 2007-06-13
• Wheeler, John A. (1990), A Journeying Into Gravity and Spacetime, Scientific American Library, San Francisco: Westward. H. Freeman, ISBN0-7167-6034-7
• Volition, Clifford M. (1993), Was Einstein Right?, Oxford University Press, ISBN0-19-286170-0
• Will, Clifford M. (2006), "The Confrontation between Full general Relativity and Experiment", Living Rev. Relativ., 9 (1): three, arXiv:gr-qc/0510072, Bibcode:2006LRR.....9....3W, doi:10.12942/lrr-2006-three, PMC5256066, PMID 28179873
• Wright, Ned (2007), Cosmology tutorial and FAQ, University of California at Los Angeles, retrieved 2007-06-12

External links [edit]

This audio file was created from a revision of this commodity dated 9 May 2021 (2021-05-09), and does non reflect subsequent edits.

Additional resources, including more advanced material, tin can be found in General relativity resources.

• Einstein Online. Website featuring manufactures on a diverseness of aspects of relativistic physics for a general audience, hosted past the Max Planck Plant for Gravitational Physics
• NCSA Spacetime Wrinkles. Website produced by the numerical relativity grouping at the National Centre for Supercomputing Applications, featuring an elementary introduction to full general relativity, blackness holes and gravitational waves

singletonvagind.blogspot.com

Source: https://en.wikipedia.org/wiki/Introduction_to_general_relativity

Share this post